

Next: Exercice
Up: DEUG STPI TD de
Previous: Exercice : rayons de
- Montrer que les fonctions
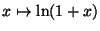 ,
,
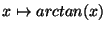 admettent un développement en série entière que l'on
précisera; on déterminera le rayon de convergence associé.
admettent un développement en série entière que l'on
précisera; on déterminera le rayon de convergence associé.
- Soit
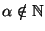 . On pose
Calculer le rayon de convergence de la série entière
. On pose
Calculer le rayon de convergence de la série entière
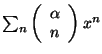 .
Soit
.
Soit 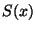 la somme de cette série. Montrer que
la somme de cette série. Montrer que 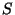 vérifie l'équation différentielle
vérifie l'équation différentielle
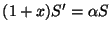 . En déduire le développement en série entière de
. En déduire le développement en série entière de
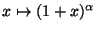 .
.
Antoine Chevreuil
2001-03-09
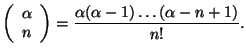
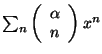 .
Soit
.
Soit 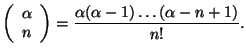
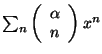 .
Soit
.
Soit