TP 4 - Compression d'image par allocation de débit (1/2)

But

Le but de ce mini-projet est de réaliser un compresseur/décompresseur d'images par allocation de débit par sous-bandes. Ce mini-projet s'étalera sur 2 TP et ce premier TP a pour but de :

réaliser et analyser une AMR 2D
étudier les propriétés statistiques des sous-bandes obtenues
utiliser ces propriétés pour estimer le coût de codage

On demande aussi de commenter les résultats obtenus et d'afficher les signaux générés à l'aide d'un outil de tracé de courbe comme gnuplot, scilab ou matlab.
Enfin, on veillera à conserver les fonctions définies ci-dessus, car elle seront réutilisées dans la suite des TPs.

Notes

Les fonctions effectuent les transformations sur place, signifiant qu'elles effectuent la transformation directement sur le signal d'entrée. Certaines opérations, comme le produit de convolution, ne sont pas possibles à réaliser directement sur place, et on pourra avoir recours à des tableaux temporaires.
Tous les signaux seront representés en C/C++ par des tableaux de double.
Un mémento des fonctions C ANSI utiles est disponible ici.

TP

1 - AMR 2D

Définition

La décomposition 2D, définie à la question 3 du TP précédent, donne une matrice faite de 4 sous-images, nommées aussi sous-bandes : l'image d'approximation et 3 images de détails (H,V et D). Tout comme en 1D, l'AMR 2D consiste en la répétition de plusieurs décompositions 2D séquentielles sur les images d'approximation.


`Lena`		`AMR 2D à 3 niveaux`

TP

Implantez la fonction amr2D_97(double* m,int p,int j) réalisant l'AMR 2D sur j niveaux, selon les filtres biorthogonaux 9/7.
Implantez sa réciproque iamr2D_97(double* m,int p,int j).
Chargez l'image lena.bmp et réalisez son AMR 2D, sur 3 niveaux.
Sauvez les coefficients, sous forme d'une image. Afin de voir quelque chose, on prendra préalablement soin pour l'image d'approximation, d'ajuster linéairement les coefficients pour qu'ils occupent la dynamique [0;255]. De même, on ajoutera 127 (gris médian) à tous les coefficients de détails.
Vérifiez objectivement que la reconstruction est parfaite.

2 - Etude des sous-bandes issues de l'AMR 2D

TP

Si on réalise une AMR 2D de niveau j, combien de sous-bandes obtient-on ?
Implantez les fonctions statistiques suivantes :

Calcul de la valeur moyenne d'une sous-bande 2D
Calcul de la variance d'une sous-bande 2D

Calculez les valeurs moyennes et les variances de chaque sous-bande obtenues par l'AMR 2D de la question précédente.
Commentez ces valeurs.

3 - Allocation de débit par sous-bande

Définition: Les variances calculées précedemment vont nous permettre d'estimer le coût de codage des différentes sous-bandes.
La relation liant le débit (en bits/pixel) nécessaire pour coder une sous-bande en fonction de la variance de cette sous-bande et des autres sous-bandes est données par :

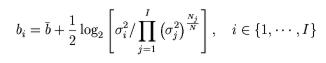
où b est le débit global alloué pour l'image.
TP: Si on désire encoder l'image avec un débit global de 1 bit/pixel (soit un facteur de compression cible de 8), calculez quels doivent être les débits de codage des sous-bandes, en utilisant la relation précédente.
Calculez ces débits de sous-bandes, pour d'autres débits globaux : 2, 0.5 et 0.25 bits/pixel.
Par curiosité, compressez lena.bmp au moyen de l'utilitaire gzip : quel facteur de compression obtient-on ?

-- Grégoire Pau - 12 Mar 2003

Retour à la page précédente