

Next: Polynômes trigonométriques
Up: DEUG STPI TD de
Previous: DEUG STPI TD de
Soit
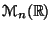 l'espace vectoriel des matrices
l'espace vectoriel des matrices 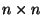 à coefficients
réels. Quelle est la dimension de
à coefficients
réels. Quelle est la dimension de
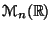 ?
Si
?
Si
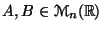 ,
on définit
,
on définit 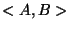 par
par
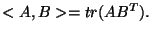 Montrer que
Montrer que 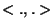 est un produit scalaire. Soit
est un produit scalaire. Soit 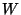 l'ensemble des matrices diagonales.
Montrer que
l'ensemble des matrices diagonales.
Montrer que 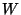 est un sous-espace vectoriel de
est un sous-espace vectoriel de
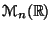 ,
et calculer sa
dimension. Caractériser le complément orthogonal de
,
et calculer sa
dimension. Caractériser le complément orthogonal de 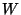 . Si
. Si 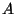 est une
matrice quelconque, calculer la projection orthogonale de
est une
matrice quelconque, calculer la projection orthogonale de 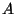 sur
l'espace
sur
l'espace 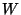 .
.
Antoine Chevreuil
2001-05-21