Matrices unitaires/hermitiennes

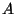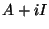Soit $A$ une matrice Hermitienne. Pourquoi $A+iI$ est-elle inversible? On considère alors

$$U=(A-iI)(A+iI)^{-1}.$$

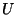Montrer que $U$ est unitaire. Montrer que 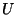$U$ est diagonalisable dans une base orthonormée et évaluer ses valeurs propres en fonction de celles de $A$.

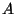Réciproquement, si 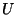$U$ est une matrice unitaire n'admettant pas 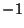$-1$ comme valeur propre, montrer que la matrice 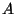$A$ définie par

$$A= i(I-U)(I+U)^{-1}$$

est Hermitienne. Exprimer 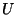$U$ en fonction de 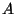$A$ et montrer que 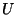$U$ est diagonalisable.