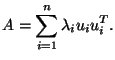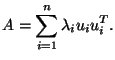

Next: About this document ...
Up: DEUG STPI TD de
Previous: Matrices unitaires/hermitiennes
Montrer qu'une matrice
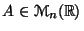 est symétrique réelle si et seulement si
il existe des réels
est symétrique réelle si et seulement si
il existe des réels
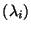 et des vecteurs
et des vecteurs 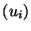 de
de
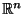 formant une famille orthonormale (relativement au produit scalaire canonique sur
formant une famille orthonormale (relativement au produit scalaire canonique sur
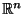 ) tels que
Si maintenant
) tels que
Si maintenant 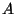 est une matrice symétrique réelle positive, montrer qu'il existe une matrice réelle symétrique positive
est une matrice symétrique réelle positive, montrer qu'il existe une matrice réelle symétrique positive 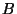 telle que
telle que
Antoine Chevreuil
2001-05-21