Une détermination de la racine carrée

1. Développer en série entière la fonction de la variable réelle 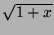$\sqrt{1+x}$. Quel est le rayon de convergence de la série?
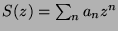2. Soit $S(z)=\sum_n a_n z^n$ la série entière précédente prolongée à 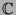$\mathbb{C}$. Montrer alors que
   $$S(z)^2 = 1+z.$$

3. En déduire que 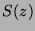$S(z)$ est une détermination de la racine carrée de $1+z$ dans le disque unité ouvert.