Fonctions holomorphes ''réelles''

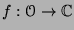Soit $f: \mathcal{O} \to \mathbb{C}$ une fonction holomorphe sur l'ouvert connexe 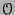$\mathcal{O}$. Montrer que les assertions suivantes sont équivalentes :

1. $f$ est constante
2. $\mathcal{R}e(f)$ est constante
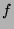3. $\mathcal{I}m(f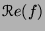)$ est constante.

En déduire que les seules fonctions holomorphes de partie réelle nulle sont des constantes.