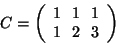

Next: About this document ...
Up: Maîtrise EEA TD d'automatique
Previous: Pendule inversé
En considérant le système d'état caractérisé par les matrices
- Montrer que le système n'est pas observable. Le mode non-observable est-il stable?
- Montrer que l'ajout d' une seconde sortie telle que
rend le système observable.
Antoine Chevreuil
2001-03-04