

Next: Stabilité des modes non-observables
Up: Maîtrise EEA TD d'automatique
Previous: Maîtrise EEA TD d'automatique
On considère un chariot homogène de masse 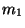 se déplaçant le long d'un axe
se déplaçant le long d'un axe
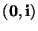 ;
un frottement visqueux de constante
;
un frottement visqueux de constante 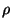 s'exerce sur ce chariot.
On fixe une barre au point
s'exerce sur ce chariot.
On fixe une barre au point 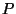 (voir figure 1) : la liaison en
(voir figure 1) : la liaison en 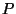 est
parfaite. On suppose en outre que la barre, de longueur
est
parfaite. On suppose en outre que la barre, de longueur 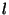 et de masse négligeable,
est assujettie à ne se déplacer que dans le
plan
et de masse négligeable,
est assujettie à ne se déplacer que dans le
plan
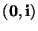 . Une masselotte
. Une masselotte 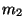 est fixée à l'extrémité de la barre.
Enfin, on appelle
est fixée à l'extrémité de la barre.
Enfin, on appelle
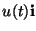 la force extérieure qui est exercé sur le chariot.
la force extérieure qui est exercé sur le chariot.
- En considérant le système
 , appliquer la relation fondamentale de la dynamique en projection sur
, appliquer la relation fondamentale de la dynamique en projection sur
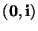 .
.
- Reprendre la question en considérant le système
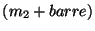 .
.
- Des équations précédentes, tirer un modèle des ``petits mouvements''.
- Proposer un modèle d'état. On considérera la sortie
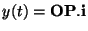
- Le système est-il asymptotiquement stable? Justifier empiriquement.
- Le système est-il observable?
Antoine Chevreuil
2001-03-04
![\includegraphics[height=4cm]{pendule.eps}](img9.gif)