Matlab toolbox for Seismic Multiple Removal (TOOLBOX_RICOCHET)
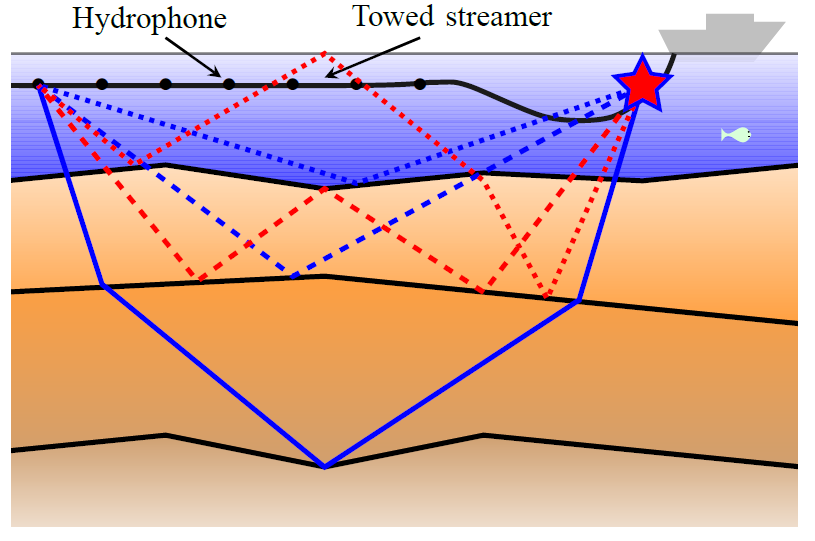
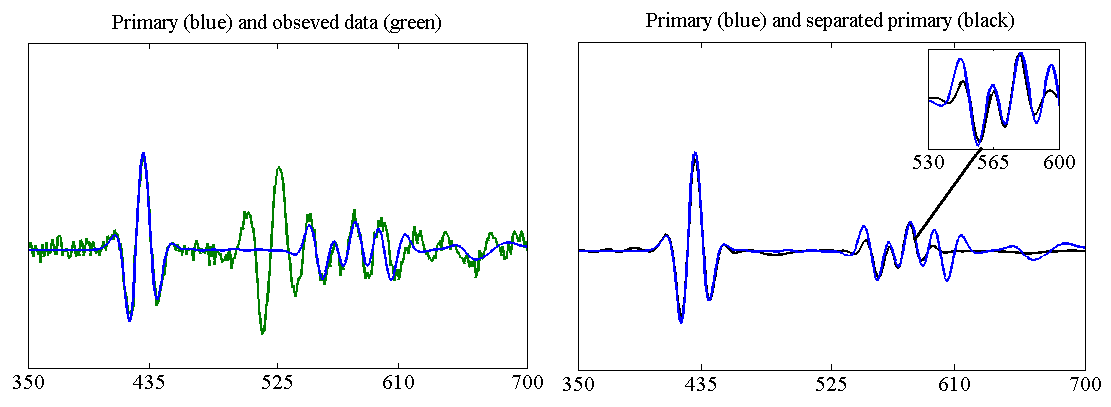
Unveiling meaningful geophysical information from seismic data requires to deal with both random and structured “noises”. As their amplitude may be greater than signals of interest (primaries), additional prior information is especially important in performing efficient signal separation. We address here the problem of multiple reflections, caused by wave-field bouncing between layers. Since only approximate models of these phenomena are available, we propose a flexible framework for time-varying adaptive filtering of seismic signals, using sparse representations, based on inaccurate templates. We recast the joint estimation of adaptive filters and primaries in a new convex variational formulation. This approach allows us to incorporate plausible knowledge about noise statistics, data sparsity and slow filter variation in parsimony-promoting wavelet frames. The designed primal-dual algorithm solves a constrained minimization problem that alleviates standard regularization issues in finding hyperparameters.

Matlab toolbox for blind deconvolution problem for sparse signals (SOOT algorithm)
This toolbox allows to solve the blind deconvolution problem for sparse signals in using a smooth approximation of l1/l2(x) as a regularization term.