Mélanges instantanés et convolutifs

Cette page est un peu plus technique et comporte quelques équations, destinées à ceux qui, un peu plus savants que les autres, continueront peut-être une lecture plus approfondie du document.

Si l'on reprend l'exemple de la figure , on peut considérer dans un premier temps que le seul trajet direct du son parvient instantanément sur les microphones. Le son est alors simplement atténué avant de s'ajouter au niveau des micros. En notant $M_{ij}$ les différents coefficients d'atténuation, $s_1(n)$ et $s_2(n)$ les signaux sources et $x_1(n)$,$x_2(n)$ les signaux reçus par les microphones, nous obtenons le modèle de mélange:

$$x_1(n) = M_{11}s_1(n) + M_{12}s_2(n)$$ (1.1)

$$x_2(n) = M_{21}s_1(n) + M{22}s_2(n)$$ (1.2)

Ce modèle de mélange instantané peut s'écrire d'une façon générale sous la forme matricielle:

$$\mathbf{x}(n) = \mathbf{M}\mathbf{s}(n)$$ (1.3)

On peut également considérer que le son subi des échos et parvient au niveau des microphones avec certains retards, de façon plus ou moins atténuée. On obtient alors un mélange de type convolutif qui s'écrit:

$$\mathbf{x}(n) = \mathbf{M}(0)\mathbf{s}(n) + \mathbf{M}(1)\mathbf{s}(n-1) + \mathbf{M}(1)\mathbf{s}(n-2) + \ldots$$ (1.4)

ou de façon encore plus générale:

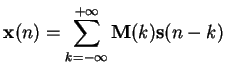$$\mathbf{x}(n) = \sum_{k=-\infty}^{+\infty} \mathbf{M}(k)\mathbf{s}(n-k)$$ (1.5)