

Next: Série entière et équation
Up: DEUG STPI TD de
Previous: Développement de fractions rationnelles
Soit la série entière
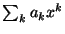 . Son rayon de convergence est supposé être
. Son rayon de convergence est supposé être 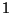 . En supposera en outre que
. En supposera en outre que
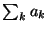 est convergente. On appellera
est convergente. On appellera 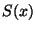 la somme de la série entière dans son domaine de convergence.
la somme de la série entière dans son domaine de convergence.
- Montrer que si
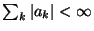 , alors
, alors 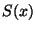 est continue à gauche en
est continue à gauche en 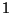 .
Nous envisageons maintenant le cas où la série
.
Nous envisageons maintenant le cas où la série 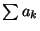 n'est pas absoluement convergente.
n'est pas absoluement convergente.
- On pose
Réecrire pour tout
![$ x \in [0,1]$](img30.gif)
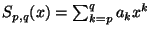 en fonction des
en fonction des 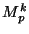 .
En déduire une majoration uniforme de
.
En déduire une majoration uniforme de
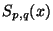 sur
sur ![$ [0,1]$](img34.gif) .
En déduire que
.
En déduire que 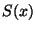 est continue en
est continue en 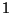 à gauche et que
à gauche et que
Antoine Chevreuil
2001-03-09